記事を書くために入試問題を見ていたら、久々に解いてみたくなりました。令和31年度の数学の問題の中から、簡単そうに見えた問2と問4をやってみました(試験問題は京都大学HPから引用)。
整数の問題は、とりあえず0、1、2、と代入してみる。
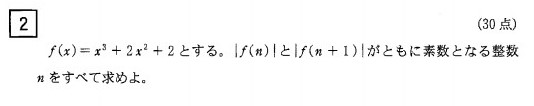
①答えがいっぱいあると2時間半で探すのが無理になるので、この手の問題の答えは数個だけです。攻略法は『数個の答えを見つけて、他にはないことを証明する』。
②素数ではないことを示すには、掛け算の形( )×( )。因数分解ができると素数ではないので証明完了です。
③0,1,2,…と順番に式に代入してみます。
0を代入するとf(0)=2で素数、
1を代入するとf(1)=5で素数、
2を代入するとf(2)=2^3+2×2^2+2=2×(2^2+2^2+1)
→( )×( )の形がでました! 証明のヒントが出たので頭に入れておきます。
(※)^は乗数表記です(2^3は2の3乗を示しています)
④マイナス側も代入してみます。
-1,-2を代入してみる→f(-1)=3で素数、f(-2)=2で素数
あとは『素数ではない』ことを示せばよさそう。
⑤f( )=2×( )の形にできそうなので、偶数を入れてみます。
n=2m(mは整数)とすると、
f(2m)=(2m)^3+2×(2m)^2+2
=2×(4m^3+4m^2+1)
=2×(4m^2×(m+1)+1)
( )の中身が2以上になると、素数ではないことを示せます。
m=1だと()の中身は2以上になります。
m=-1だとF(2m)=2×(4×(-1)^2×(-1+1)+1)=2×(4×0+1)=2で素数。
|m|≧2のとき、|4m^2|≧16、|m+1|≧1だから|4m^2×(m+1)+1|≧15。
ということで、|m|≧2(|n|=2|m|≧4)なら( )の中身は2以上になり、素数ではないことを示せました。
⑥次はnが奇数の時。
nが-5以下または3以上の奇数のとき、n+1は絶対値4以上の偶数になるので|f(n+1)|は素数になりません。
n=-3だけ検証できてないから代入して計算すると、計算|f(-3)|=7で素数になりました。
-4以上2以下で|f(n)|が素数になるnは-3,-2,-1,0,1。n=1だとf(n+1)=f(2)が素数でないので、|f(n)|と|f(n+1)|がともに素数になるのはn=-3、-2、-1、0
確率の問題は『全部同じになる確率』か『1回も出ない確率』に近づける。

サイコロを1回振って1が出る確率は1/6。
2回振って2回とも1が出る確率は1/6×1/6=1/36。
3回振って3回とも1が出る確率は1/6×1/6×1/6=1/218。・・・
サイコロを1回振って1が出ない確率は5/6。
2回振って2回とも1が出ない確率は5/6×5/6=25/36。
3回振って3回とも1が出ない確率は5/6×5/6×5/6=125/218。・・・
『全部1になる』確率と『1回も出ない』確率は単純な掛け算になります。だから、どちらかに近づけるように狙うと攻略しやすくなります。
①1回目が4以下で2回目が5以上になる確率は、4/6×2/6=2/9。
そうならない確率は、1-2/9=7/9。
②3回振った時に、2回目が4以下で3回目が5以上にならない確率は7/9。
3回振って、Xk-1≦4かつXk≧5が1回も起きない確率は、7/9×7/9。
あとはサイコロを振る回数だけ掛け算していけばよいので、掛ける回数だけ気をつけてn回目に『1回も起きない確率』を計算します。
n回振った時に、Xk-1≦4かつXk≧5が1回も起きない確率は、(7/9)^(n-1)。
③問題文を読むと、n回振った時に1回だけ『k-1回目が4以下でk回目が5以上になる』とあります。
1回目が4以下で2回目が5以上になる確率は2/9。2回目以降にサイコロを振ったn-1回が全部外れる確率は(7/9)^(n-2)なので、1回目2回目だけ条件を満たす確率は2/9×(7/9)^(n-2)。
何回目に出るかはn-1通りあるので、1回だけXk-1≦4かつXk≧5が出る確率は(n-1)×2/9×(7/9)^(n-2)。
2回目が5以上になると3回目に何が出てもNGになるところが反映できているかがちょっと怪しいですが、何となくは解けました。10分くらいで『どうやったら解けるか』が見えてきて、1時間弱で2問解けたので数学だけならまだ通用しそうです。
知っているから解ける。
さて、世の中には上記の問題を初見でスラスラ解けてしまう人もいます。しかし、ほとんどの人はできないと思います。私も『最初からできた』訳ではありませんでした。今、私が問題を解けた理由はただ一つ。やり方を知っていたから。
過去問や想定問題集を見て、解答例を読む。理解できないことがあったら先生に聞いて、自分でやってみて解けるか確認する。正解までたどり着けたら、何回も復習して覚える。そうやって『解ける問題』を増やしていくと、初見の問題でも『過去に解いたことがある似たような問題』を基にして攻略方法が見えてくるようになります。このあたりのことは、後日改めて記事にしたいと思います。




コメント